
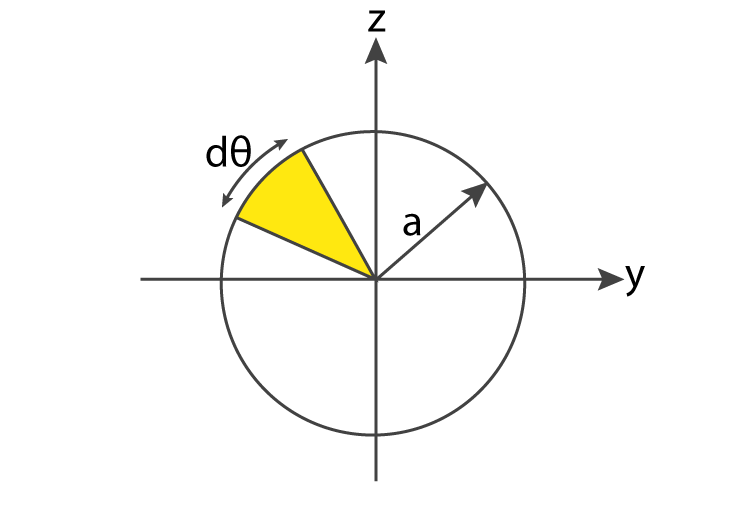
The International System of Units or SI unit of the moment of inertia is 1 kilogram per meter-squared. Refer to (Figure) for the moments of inertia for the individual objects. The calculation for the moment of inertia tells you how much force you need to speed up, slow down or even stop the rotation of a given object. In both cases, the moment of inertia of the rod is about an axis at one end. In (b), the center of mass of the sphere is located a distance R from the axis of rotation. In (a), the center of mass of the sphere is located at a distance L+R from the axis of rotation. A closed geometry formed by the positioning of points that makes a half image of a complete circle in a one-dimensional plane is called a semicircle. Since we have a compound object in both cases, we can use the parallel-axis theorem to find the moment of inertia about each axis. The radius of the sphere is 20.0 cm and has mass 1.0 kg. The rod has length 0.5 m and mass 2.0 kg. This means that if a single mass of `7` kg was placed `2.6` m from the `x`-axis, this would have the same moment of inertia as the original shape when rotating around the `x`-axis.Find the moment of inertia of the rod and solid sphere combination about the two axes as shown below. `A=int_1^2 (x^2+1) dx - 1` (We need to subtract the area of the `1xx1=1` square below the shaded area.) D.3-4 Determine the moment of inertia I, of a circle of radius r with. We use a computer algebra system to obtain: D.3-2 Determine the moment of inertia I be of a trapezoid having bases a and b. `x_1= sqrt(y-1)` (the curve closest to the `y`-axis), and `x_2= 2` (the "curve" furthest from the `y`-axis), So the required values which we can use in the formula are: We take the positive case only, as we are dealing with the first quadrant. Since we started with `y=x^2+1`, we solve for `x` and obtain: We need to express our function in terms of `y`.
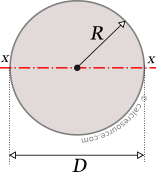
In this example, we are rotating the area around the `x`-axis. The shaded area is the part that's rotating around the `x`-axis, and we have indicated a "typical" rectangle. Rotation about the x-axisįor rotation about the x-axis, the moment of inertia formulae become:įind the moment of inertia and the radius of gyration for the area `y=x^2+1` from `x=1` to `x=2`, and `y>1`, when rotated around the x-axis. This means that if a mass of `(2k)/3` was placed `0.447` units from the `y`-axis, this would have the same moment of inertia as the original shape. Here, R is the radius and the axis is passing through the centre. `y_2= 1 − x^2`, and `y_1= 0`, `a = 0` and `b = 1`. Moment of inertia of a circle or the second-moment area of a circle is usually determined using the following expression I R 4 / 4. It's a parabola, passing through (1, 1) and (0, 1). the origin (0,0) of a system which has masses at the points given: MassĪs usual, first we sketch the part of the curve in the first quadrant. So that should make sense, were dividing by the moment of inertia, were dividing by the rotational inertia because that means if this rotational inertia is big, look it, this is in the denominator. Example 1įind the moment of inertia and the radius of gyration w.r.t. Calculate the moment of inertia of the ball about. Area Moment of Inertia Section Properties Solid Round Calculator. If we wish to place all the masses at the one point ( R units from the point of rotation) thenĭ 1 = d 2 = d 3 =. A small 520-gram ball on the end of a thin, light rod is rotated in a horizontal circle of radius 1.5 m. Area Moment of Inertia Section Properties I. d n, (respectively) from the point, then the moment of inertia I is given by: , m n is rotating around a point with distances d 1, d 2, d 3. If a group of particles with masses m 1, m 2, m 3. The moment of inertia of a particle of mass m rotating about a particular point is given by: The moment of inertia is a measure of the resistance of a rotating body to a change in motion.


 0 kommentar(er)
0 kommentar(er)
